在物理世界中,物体经常以有序的方式彼此推开。试想一下铁屑在磁场的作用下形成的对称样式,或者是行人均匀的社交距离。
当数学家查看数轴时,他们会看到相同类型的趋势。他们查看表示正数和负数的刻度线,并感觉到一种数字力,使它们保持相等的间距。就好像领土辽阔的山狮们一样,整数彼此之间的距离不能比1个单位还近。
数轴上的间距是在整个数论领域中被发现的现象的最基本示例。它出现在素数的研究以及不同类型方程的解之间的关系中。数学家可以通过量化它们之间的作用力来更好地理解这些重要值。
具有数论意义的事物趋于彼此推开。多伦多大学的Jacob Tsimerman说。“我们尝试获得排斥原理(repulsion principles),并用它们来获得其他各种结果。”
数论中的许多重要结果与排斥原理如何影响多项式,系数和变量的幂的方式有关。几十年来,数学家一直在努力确定这种情况下的排斥力的确切大小。
十二月底在网上发布的一个证明中,多伦多大学的Vesselin Dimitrov终于做到了。
剑桥大学的Péter Varjú在电子邮件中说:“这真是太壮观了。” “ Vesselin的想法是全新的,而且很漂亮。”
Dimitrov解决的问题(称为Schinzel-Zassenhaus猜想)与多项式值的几何有关。它可以预测,当绘制某些值的图形时多项式的定义,它们将以精确的方式散布,看起来就像彼此推开了一样。Dimitrov的工作精确地量化了这种扩散,证明了这一猜想是正确的。它还提供了对数字似乎遵循的定律的新见解。
Tsimerman说:“这一结果为我们对代数数的理解之地上又插上了一枚旗帜。”
单位根(The Roots of Unity)
在研究多项式时,数学家对它们的“根”特别感兴趣,“根”是使多项式等于零的变量的值。多项式的根数与其次数,即最大指数的值一样多。所以x² – 4具有两个根(2和-2),而x⁵ – 7x³+ 2x² – 4x – 9有五个根。
数学家想知道多项式的根是如何相互联系的。例如,在绘制图形时,某些多项式的根恰好落在规则多边形的顶点上-它们以精确的几何长度分开。数学家对找到根之间的其他更微妙的几何关系感兴趣。
“你可以获得哪种模式?你能得到任何模式,或者模式受到某种限制吗?” 剑桥大学的Emmanuel Breuillard说。
Dimitrov解决的问题涉及一个称为分圆多项式(cyclotomic polynomials)的特别重要的表达式族的根。这些多项式不能分解为较小的多项式,但是你可以使用它们来构建其他多项式,它们就像多项式的元素周期表中的元素。第一个也是最简单的分圆多项式是x − 1,第二个是x +1。第十个是x⁴− x³+ x² − x +1。但是,与元素周期表不同,分圆多项式的列表永远持续下去。
分圆多项式的根遵循非常特殊的几何图案。要查看它,请从空白的复平面开始,其中x轴绘制实数,y轴绘制虚数。然后在原点周围刻一个半径为1的圆。这是单位圆。分圆多项式的根都位于该圆上。他们有一个优雅的名字:“单位根”(roots of unity)。
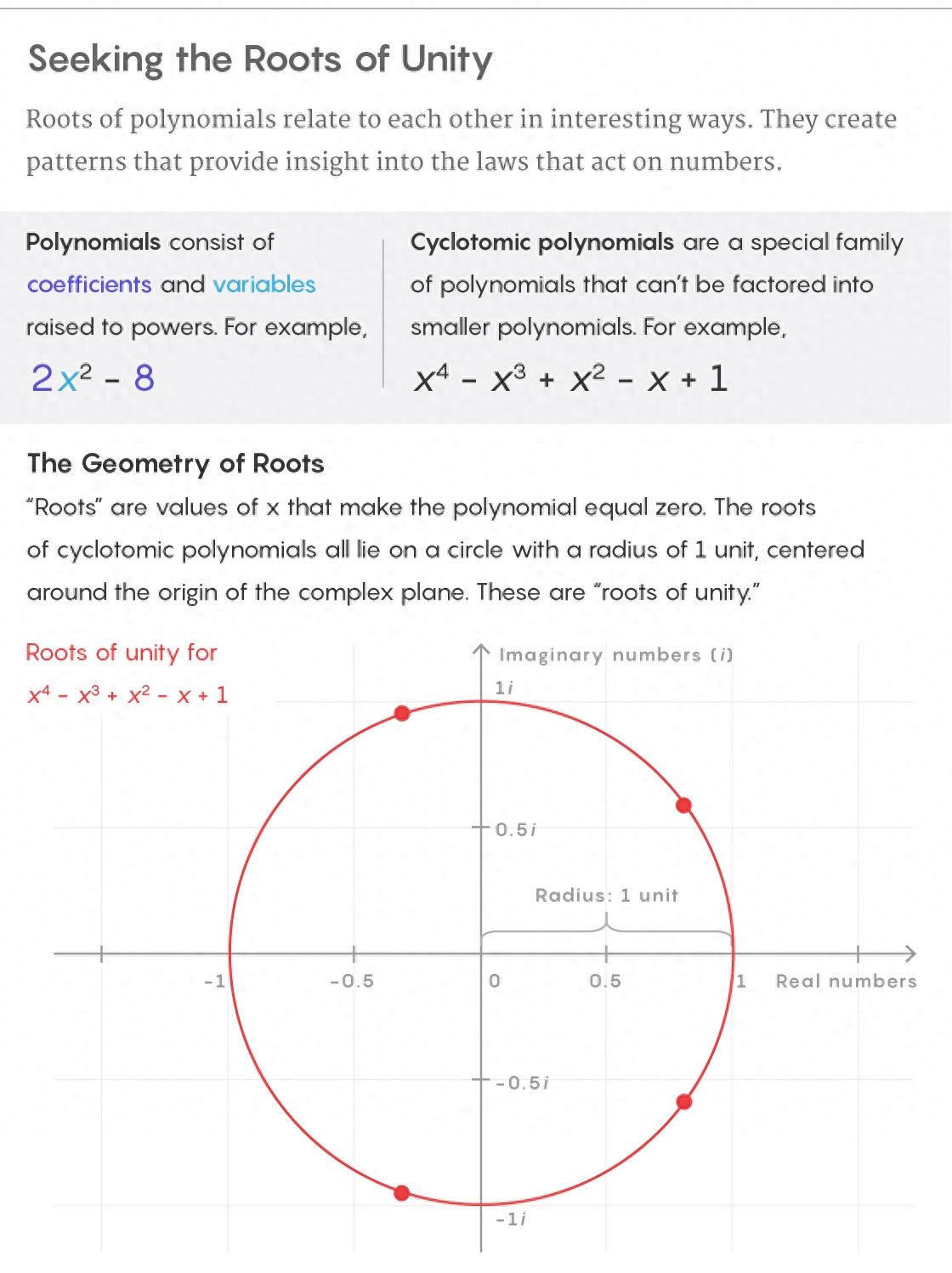
Quanta杂志的5W信息图;资料来源:Alex Kontorovich
但是大多数多项式都是非分圆的,它们的根不是单位根。几乎你遇到的所有系数,变量和指数的组合都是这种情况。
1965年,Andrzej Schinzel和Hans Zassenhaus预测,分圆多项式和非分圆多项式的根的几何形状在非常特定的方面有所不同。取任何一个首项系数为1的非分圆多项式,画出其根。有些可能落在单位圆内,有些可能就落在单位圆上,还有一些可能落在单位圆外。Schinzel和Zassenhaus预测,每个非分圆多项式都必须至少有一个单位圆之外的根,并且至少要有最小的距离。
或者,以斥力来表示Schinzel-Zassenhaus猜想,它预测非分圆多项式的最小根(可能落在单位圆内)有效地将其他根推到单位圆外,就像磁铁彼此推开一样。
“你可以将多项式的根视为带负电荷的粒子,它们之间的排斥力随着距离的增加而衰减,” Breuillard说。
Schinzel-Zassenhaus猜想甚至精确地定义了排斥力应该有多强。Tsimerman说:“它表示存在一种非常精确的,可量化的含义,即根不能都非常接近单位圆。”
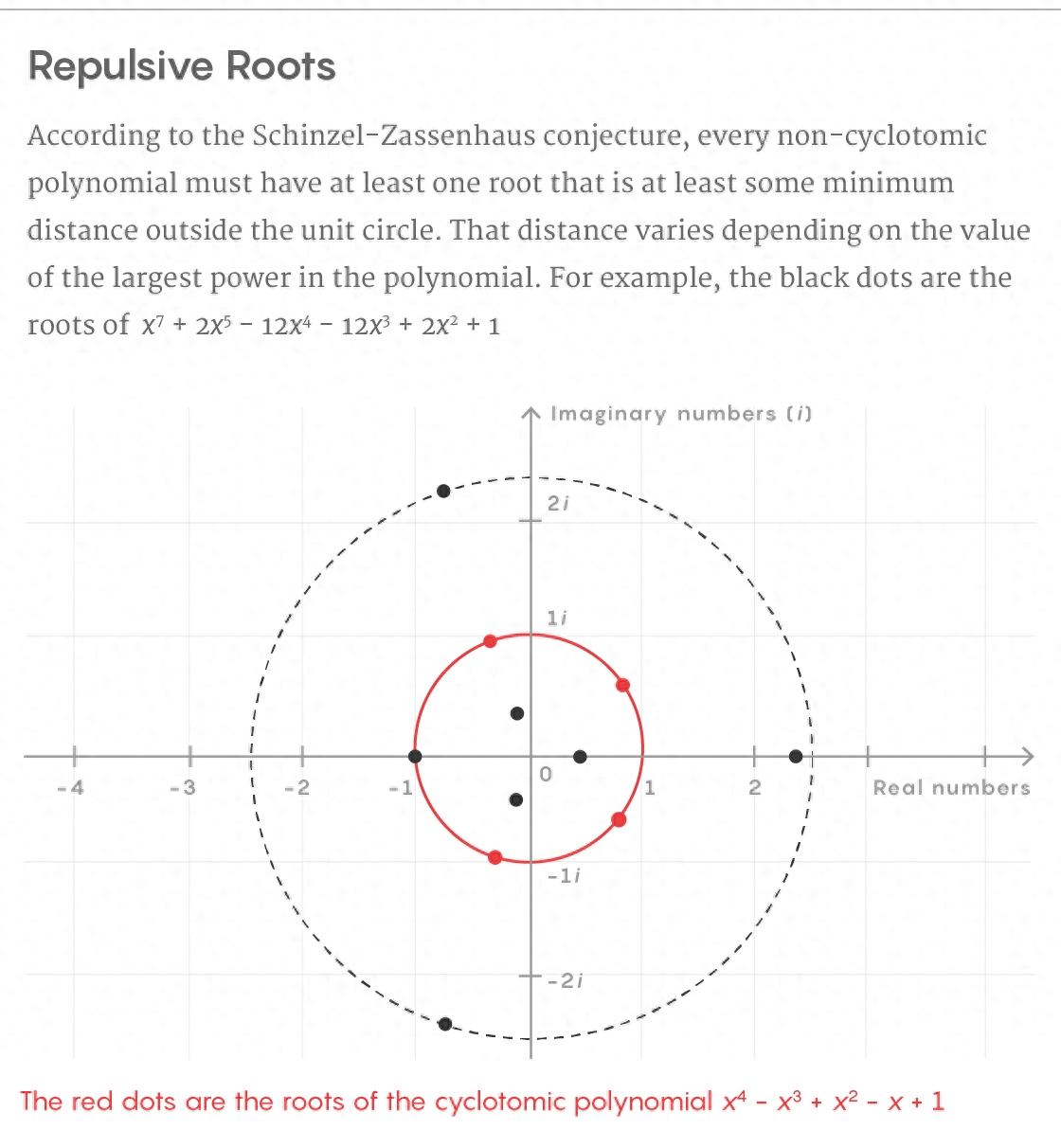
Quanta杂志的5W信息图;资料来源:Alex Kontorovich
此猜想的主要预测具有物理学方程式的感觉。它说每个非分圆多项式都应至少有一个在单位圆之外的根,该根的距离等于一个常数除以多项式的次数。该常数的确切值并不严格,因此举个例子,假设它是0.1。如果我们有一个23次的非分圆多项式,则推测它在单位圆之外的根至少应为0.1 / 23。
这是一个有力的陈述,但是数十年来,数学家仅设法确认了猜想预测的较弱版本。
Schinzel和Zassenhaus自己证明,每个非分圆多项式,有一个根至少落在单位圆外1/4ᵈ处(其中d是多项式的次数)。由于分母中存在指数,因此该距离比猜测的距离小得多。
在接下来的三十年中,数学家对Schinzel和Zassenhaus的工作进行了一系列改进,但进展仍不完全。数学家认为正确的距离应该是一个尺寸,但是他们只能证明它至少是一个较小的尺寸。假设能被最终解决,数学家们不知道解决Schinzel-Zassenhaus猜想难度有多大。
Dimitrov在电子邮件中说:“一开始,人们永远都不知道一个问题的解到底是简单还是复杂,直到找到解为止。”
聪明的重组
通常,一个突出的数学问题长时间未解决,是因为数学家只是缺乏解决该问题所需的技术。梦想飞向月球,直到有人发明了火箭,你才到达那里。
但是事实证明,这个问题是不同的。“这项技术已经存在了至少40年,” Tsimerman说。
Dimitrov将有关多项式根大小的问题转换为相关但不同类型的数学对象(称为幂级数)值的大小的问题。幂级数就像多项式,只不过有无限多项。
芝加哥大学的Frank Calegari在电子邮件中说:“正如数学中经常发生的那样,关键的见解/突破是将两个看似不同的问题联系起来。”
数学家习惯于在多项式和幂级数之间轻松移动,并使用一个函数的性质建立另一个函数的性质,但是Dimitrov之前的数学家并未想到使用这种对应关系来解决Schinzel-Zassenhaus猜想。
为了证明他想证明的多项式,Dimitrov需要相关的具有特定的基本属性的幂级数:所有系数都必须是正整数或负整数(因此没有小数)。当Dimitrov开始这项工作时,没有明显的方法可以保证会发生这种情况。
但是在2019年11月,Dimitrov在“浏览几本代数组合学书籍和论文”时多项式的定义,意识到有一种方法可以将一些众所周知的定理拼凑起来,以在非分圆多项式与其幂级数之间产生正确的关系。他采用了一个非分圆多项式,找到了它的根,将那些根提高到不同的幂,将它们相乘,然后取该乘积的平方根。然后最终他可以基于该平方根构造具有基本性质的幂级数。
Dimitrov说:“对我来说,这是一个令人惊讶的技巧,因为我们取该乘积的平方根。” 一切都出乎意料且很有帮助,Dimitrov称其为“小奇迹”这一事实。这样就可以进行他的下一步证明。
Dimitrov证明了幂级数的系数是整数。从某种意义上讲,它们始终很“大”(必须至少为1)。因此,与幂级数相关的其他值(其“Hankel行列式”)也必须很大。通过仔细的论证,他证明了如果系数是整数并且Hankel行列式很大,那么他开始使用的非分圆多项式的根之一也必须很大。证明的大部分工作都是严格证明这种联系。
“系数不小的含义意味着Dimitrov寻求的东西非常微妙。这不是直接推断出来的事情,”比萨高等师范学校的Umberto Zannier说。
Dimitrov证明,所有非分圆多项式,至少有一个根落在单位圆外 log 2除以多项式次数的四倍处。即(log 2)/(4 d)。Dimitrov的结果满足了Schinzel和Zassenhaus的预测,即距离是某个常数除以多项式次数的函数。他通过找到一种新颖的方法来重新组合数学家已经拥有的工具,从而做到了这一点。
Zannier说:“他发明了一种被完全隐藏的证明模式。” “这些片段早已被证明,但是这些片段都早先存在于与Schinzel-Zassenhaus无关的理论中。”
Dimitrov的证明解决了数论中关于多项式中出现的模式的主要问题之一。未来的工作可能会是调整Dimitrov提出的比率。确切的值可能是分子中的log 3,以及分母中多项式的次数的5倍。但是对于数学家来说,常数的确切值只是一种技术问题。最重要的是比例,从这个意义上讲,Dimitrov准确地证实了辛泽尔(Zinzel)和扎森豪斯(Zassenhaus)的预测。
“这个结果非常清晰,这是最好的结果,” Breuillard说。“没有比这更好的了。”
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: Lgxmw666






