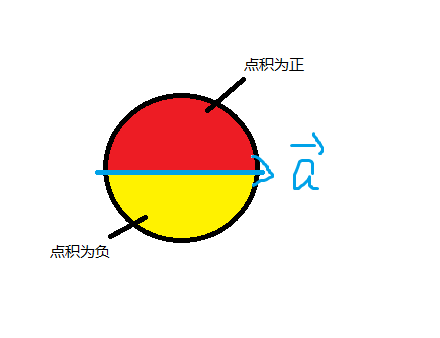
任给 n 维单位向量 a, 随机产生符号向量 x(每个分量等概率取 1 或 -1),猜想 :,其中 Prob() 表示概率。
此为符号与单位向量内积猜想,也称为托氏猜想(Tomaszewski猜想)。1986年4月Richard Guy发表于《美国数学月刊》的论文[1]中首次提出该猜想,并归功于Boguslav Tomaszewski。该猜想有一个等价的几何版本:
一个n维超立方体的内接球的平行支撑超平面可以夹住该超立方体至少一半的顶点。
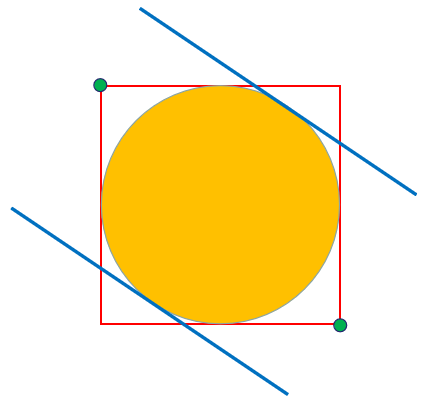
以n=2为例,如下图所示,正方形有4个顶点,内接圆的任意两条平行切线至少夹住2个顶点,当平行线与正方形边重合时夹住4个顶点。

托氏猜想自提出以来广为关注。1992年,Holzman和Kleitman[2]证明了概率下界至少为3/8=0.375,该记录一直保持到2017年才被Boppana和Holzman[3]打破,下界改进到0.406;2020、2021年学者们进一步改进到0.427[4]和0.46[5],被证明的下界逐渐接近0.5。另一条证明路线是依次证明n=2,3,4… 成立,比如2017年[6]证明了n≤9时猜想成立。还有一条路线是证明对最小的b成立,[7]提到了。值得一提的是,Hiriart-Urruty 2008年将该猜想列为优化与矩阵分析9个公开问题中的第8个[7](有趣的是向量的内积,Hiriart-Urruty在2007年[8]中提了14个公开问题,这样“凑”出了优化23个公开问题)。
2022年5月底向量的内积,以色列巴伊兰大学数学系两位学者N.Keller和O.Klein彻底证明了托氏猜想,论文发表在Advances in Mathematics[9]。
托氏猜想(现需改称托氏定理,Tomaszewski定理)在优化中的应用最早追溯到三位国际知名专家Ben-Tal, Nemirovski和Roos在2002年发表的著名论文[10],该论文在未知托氏猜想的前提下,独立提出了该猜想,并且独立证明了1/3的概率下界。此外,该论文还提出了更一般的猜想:
对任一 n 阶对称矩阵 B,随机产生符号向量 x(每个分量等概率取 1 或者 -1),总成立。

当B是半正定且秩为1时,上述猜想退化成托氏定理。
论文[10]证明了的下界,并作为应用分析了齐次二次约束二次非凸优化的半定规划算法的近似比。2008年何斯迈教授、罗智泉院士、聂家旺教授、张树中教授[11]首次证得0.03的常数下界。同年,该下界被改进成0.0309[12]。2013年,袁亚湘院士用一个简单的例子(n=6, B为元素全为-1的矩阵,相应的概率证伪了Ben-Tal,Nemirovski,Roos的猜想[13]。
2022年,在戴彧虹研究员的指导下,中国科学院大学的本科生杨景添同学构造了如下一个概率为3/16的具体例子:(左右滑动查看完整内容)
笔者开设的《数学软件》课程中对矩阵情形的猜想布置了大作业,北航数学科学学院的本科生岳泽阳同学利用数值模拟的方法,算得概率为3/16的例子。
参考文献
[1] R.K. Guy, Any answers anent these analytical enigmas? Am. Math. Mon. 93(4), (1986) 279-281.
[2] R. Holzman, D.J. Kleitman, On the product of sign vectors and unit vectors, Combinatorica 12(3), (1992) 303-316.
[3] R.B. Boppana, R. Holzman, Tomaszewski’s problem on randomly signed sums: breaking the 3/8 barrier, Electron. J. Comb. 24(3), (2017) P3.40.
[4] R.B. Boppana, H. Hendriks, M.C.A. van Zuijlen, Tomaszewski’s problem on randomly signed sums, Electron. J. Comb. 28(2), (2021) P2.35.
[5] V. Dvořák, P. van Hintum, M. Tiba, Improved bound for Tomaszewski’s problem, SIAM J. Discrete Math. 34(4), (2020) 2239-2249.
[6] H.Hendriks, M.C. Zuijlen, Linear combinations of Rademacher random variables. arXiv:1703.07251 (2017)
[7] Hiriart-Urruty, J.B., A new series of conjectures and open questions in optimization and matrix analysis.ESAIM: Control Optim. Calc. Var., 15, (2008) 454-470.
[8] Hiriart-Urruty, J.B., Potpourri of Conjectures and Open Questions in Nonlinear Analysis and Optimization, SIAM Rev., 49(2),(2007) 255-273.
[9] N.Keller, O. Klein, Proof of Tomaszewski’s conjecture on randomly signed sums, Adv. Math., 407, 2022, 108558.
[10] Ben-Tal A., Nemirovski A., Roos C., Robust solutions of uncertain quadratic and conic quadratic problems, SIAM J. Optim., 13(2), (2002) 535-560.
[11] He S.,Luo Z.-Q., Nie J., Zhang S., Semidefinite relaxation bounds for indefinite homogneous quadratic optimization, SIAM J. Optim.,19, (2008) 503-523.
[12] Veraar M., A note on optimal probability lower bounds for centered random variables,Colloq. Math., 113, (2008) 231-240.
[13] Yuan Y.-x.: A Counter-Example to a Conjecture of Ben-Tal, Nemirovski and Roos, J. Oper. Res. Soc. China, 1,(2013) 155-157.
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: Lgxmw666