复正弦函数余弦函数
正弦函数和余弦函数,是我们中学里学过的有界的周期函数,余弦函数图像可以看成是正弦函数图像向右平移得到,正弦函数是奇函数,通过原点,余弦函数是偶函数,正弦函数和余弦函数都有最大值1,最小值-1.如果将自变量扩展到复数的情况,复变量的正弦函数和余弦函数定义如下:
这个定义将指数函数和三角函数联系起来了,1740年10月18日,欧拉给伯努利的信中,求解一个二阶常系数的微分方程初值问题,通过计算给出的解是y(x)=2cosx,欧拉把这个解也用exp(ix)+exp(-ix)表示了,并且标注了正弦函数2isinx=exp(ix)-exp(-ix),1748年,欧拉第一次给出了欧拉公式如下:
上面欧拉公式推广到复数形式可以得到
上面的正弦余弦函数定义,可以看成从上面两个复指数函数方程中解出来的。
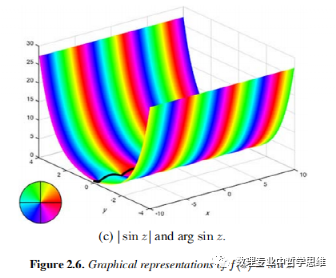
下面给出了复变余弦函数的实部,虚部,模和辐角的图形如下:
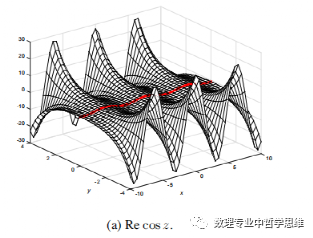
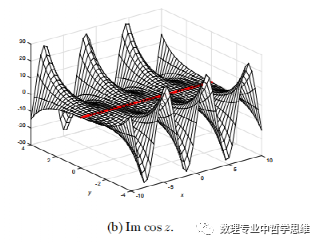
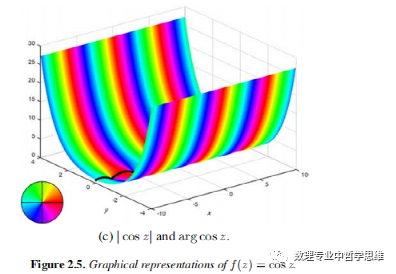
从图像中可以看出正弦值,实部和虚部都是沿着x轴成周期性变化的,y越大,实部和虚部的最大值就越大,最小值就越小,从模和辐角的图像可以看出来,余弦函数不再是有界的了。余弦函数在整个复平面上处处解析。
下面给出了正弦函数的图像,

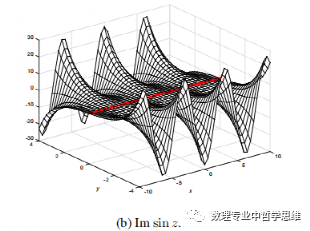
复变量的正弦函数是奇函数,是沿着x轴周期变化的,没有最大值和最小值正弦值,在整个复平面上处处都是解析的。
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: Lgxmw666
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。