第二数学归纳法-我对「数学归纳法」的理解

1、

「数学归纳法」是一种数学证明方法。

当我们需要证明一个命题对所有自然数（正整数）都成立，就会用到它。

2、

数学归纳法有两个步骤：

（1）证明 当 n = 1 （开头那个数）时，命题成立。

（2）假设 当 n = k 时第二数学归纳法，命题成立。

证明 当 n = k+1 时，命题也成立。

步骤一很简单，直接把 n = 1 往式子里带，算式肯定成立（

）。

难点在步骤二。

大家如果对高中数学还有印象的话就知道，我们在证明 n = k+1 的时候是可以直接使用 n = k 这个假设的。

「用假设的方式去证明」，这听起来……怎么感觉「数学归纳法」不是很严谨啊？

它其实是严谨的。

3、

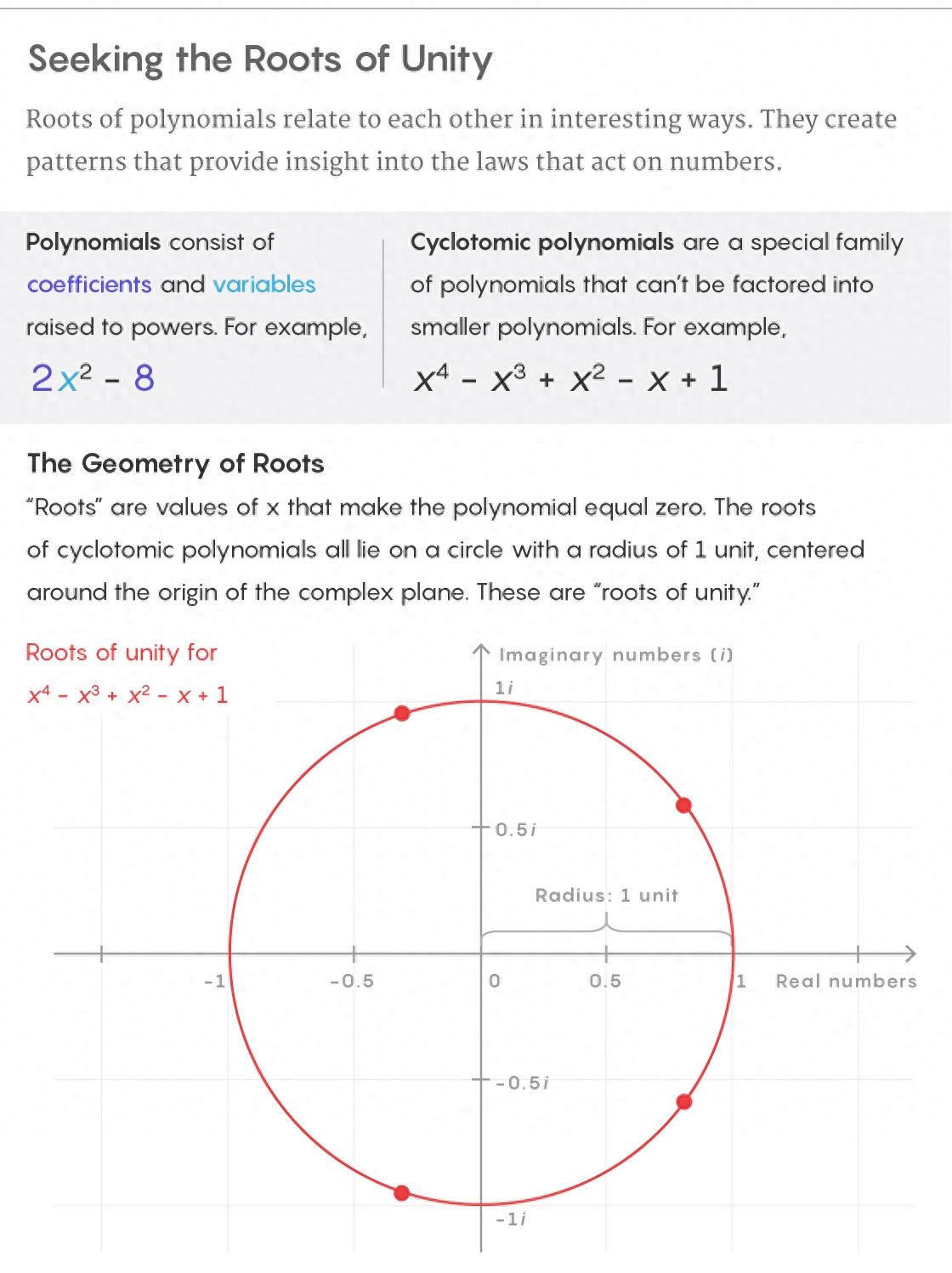
我们可以将「数学归纳法」可以理解为：「多米诺骨牌效应」。

刚才说了，数学归纳法做的事情是：证明一个命题对所有正整数都成立。

对应到「多米诺骨牌」，就相当于是让所有骨牌都倒下。

4、

怎样才能让所有骨牌都倒下？

我们得把骨牌的位置给摆放好第二数学归纳法，确保一件事：只要有一个骨牌倒下了（无论是哪一个骨牌），它一定会连累到后面的骨牌让其也倒下。这就是数学归纳法的「步骤二」：

（2）假设当 n = k 时，命题成立。

证明当 n = k+1 时，命题也成立。

当然了，光把骨牌摆放好还是不够的，毕竟我们的目标是让所有骨牌都倒下。所以我们还得把第一个骨牌推一下，才能实现这个目标。

也就是数学归纳法的「步骤一」：

（1）证明当 n = 1 （开头那个数）时，命题成立。

5、

前几天看到谢老师发的一条微博，分享给大家：

———END———
限 时 特 惠： 本站每日持续更新海量各大内部创业教程，一年会员只需98元，全站资源免费下载 点击查看详情
站 长 微 信： Lgxmw666