哈喽,大家好!我们又见面了,欢迎继续关注【轩爸辅导】的【口袋数学】。日更【每日一学】【每日一练】,帮助孩子日积月累,考出好的成绩。配套辅导多项式的定义,哪里不会学哪里,哪里出错练哪里,帮助孩子提高效率。

01 知识要点归纳要点一、单项式
1.单项式的概念:
单独的一个数或一个字母也是单项式.
要点诠释:(1)单项式包括三种类型:①数字与字母相乘或字母与字母相乘组成的式子;②单独的一个数;③单独的一个字母.
(2)单项式中不能含有加减运算,但可以含有除法运算.
因为它无法写成数字与字母的乘积.
2.单项式的系数:单项式中的数字因数叫做这个单项式的系数.
要点诠释:(1)确定单项式的系数时,最好先将单项式写成数与字母的乘积的形式,再确定其系数;
(2)圆周率π是常数.单项式中出现π时,应看作系数;
(3)当一个单项式的系数是1或-1时,“1”通常省略不写;(4)单项式的系数是带分数时,通常写成假分数,
3.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
要点诠释:单项式的次数是计算单项式中所有字母的指数和得到的,计算时要注意以下两点:
(1)没有写指数的字母,实际上其指数是1,计算时不能将其遗漏;
(2)不能将数字的指数一同计算.
要点二、多项式
1.多项式的概念:几个单项式的和叫做多项式.
要点诠释:“几个”是指两个或两个以上.
2. 多项式的项:每个单项式叫做多项式的项,不含字母的项叫做常数项.
要点诠释:(1)多项式的每一项包括它前面的符号.
(2)一个多项式含有几项,就叫几项式,
3. 多项式的次数:多项式里次数最高项的次数,叫做这个多项式的次数.
要点诠释:(1)多项式的次数不是所有项的次数之和,而是多项式中次数最高的单项式的次数.(2)一个多项式中的最高次项有时不止一个,在确定最高次项时,都应写出.
4.升幂排列与降幂排列: 把一个多项式按某一个字母的指数从大到小的顺序排列起来,叫做把多项式按这个字母降幂排列;若按某一个字母的指数从小到大的顺序排列起来,叫做把多项式按这个字母升幂排列.

要点诠释:
(1)重新排列多项式时,每一项一定要连同它的正负号一起移动;
(2)含有两个或两个以上字母的多项式,常常按照其中某一个字母的升幂排列或降幂排列.
要点三、同类项
定义:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.几个常数项也是同类项.
要点诠释:
(1)判断是否同类项的两个条件:①所含字母相同;②相同字母的指数分别相等,同时具备这两个条件的项是同类项,缺一不可.
(2)同类项与系数无关,与字母的排列顺序无关.
(3)一个项的同类项有无数个,其本身也是它的同类项.
02 典型例题讲解
例1、(2015•巴中)
A. a=3,b=1 B. a=﹣3,b=1 C. a=3,b=﹣1 D. a=﹣3,b=﹣1
【答案】 A
【分析】利用同类项的定义列出方程组,求出方程组的解即可得到a与b的值.

故选A.

03 举一反三练习

04 参考答案解析
1、【答案】 C
【分析】根据多项式次数的定义得到n-2=3,解得:n=5。
故选C。
2、【答案】 D
【分析】利用同类项的定义判断即可.
【解答】解:不是同类项的是a2b3与﹣a3b2 .
故选:D.
3、【答案】解:
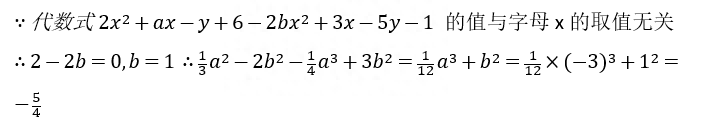
【分析】将代数式进行合并同类项,根据与字母x的取值无关,可得关于x的多项式的系数均为0,可求得a和b得数值,降其代入代数式中求值即可。
4、【答案】1;2
【分析】多项式的次数是次数最高项的次数,所以该多项式的各项次数不大于2,对于次数大于2的项应该令其系数为0;而剩余的两项一个次数为n,一个次数为1多项式的定义,所以必须有n=2.
【解答】因为多项式(m-1)x3-2xn+3x的次数是2;所以三次项不存在即m-1=0,-2xn这一项的次数为2从而m=1,n=2.

———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: Lgxmw666






