
,数学本来很有趣
圆有多重要,观察生活中圆的应用场景就能体会到:手机的摄像头、汽车的方向盘、车轮、房子的屋顶、喝水的杯子、炒菜的锅、精美的瓷器……
从圆的绘制过程可以看出,圆心决定了圆的位置,半径(或直径)决定了圆的周长和面积。
圆的周长=πD=2πr
圆的面积S=πr²
n°的扇形的面积S=n/360×π×r²
-1-
重叠法与割补法
规则的图形可以直接利用公式求解。不规则的图形,往往需要将图形拆分、移动和重组,拼成规则的图形,然后再利用规则图形的相加或相减来进行求解。
方法一『阴影=整体-空白』:
阴影不规则,整体和空白是规则的。
方法二『重叠法』:
利用容斥原理,有重叠的部分相加-整体=重叠的部分
方法三『割补法』:
通过拆分和重组,把不规则的图形拼成规则的图形。
如何把不规则的图形,通过拆分和重组,变成一个规则的图形,是解此类问题的关键。
-2-
例题与分析
例1.
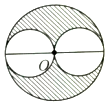
如图,在一块面积为12.56平方厘米的铝板中,裁出了2个同样大小的圆铝板。问:余下的总面积是多少平方厘米?(π取3.14)
解析:
阴影是不规则的,但是整体和空白的部分都是规则的圆。利用公式“阴影=整体-空白”。
整体的面积12.56,所以大圆的半径R²=12.56÷π=4,所以大圆的半径R=2。
小圆的半径等于大圆半径的一半=2÷2=1。
所以阴影面积=πR²-2πr²=4π-2π=2π=6.28平方厘米
例2.
如图,正方形的边长为4,求阴影的面积。(π取3.14)

解析:
观察图形不难看出,阴影的部分是两个扇形交叉的重叠部分。
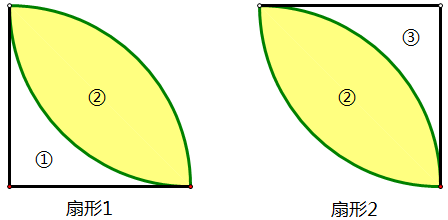
扇形1的面积=①+②
扇形2的面积=②+③
正方形的面积=①+②+③
利用容斥原理,阴影②的面积=扇形1+扇形2-正方形
图中的两个扇形的面积和正好等于一个半圆。正方形的边长=扇形的半径。
所以,阴影的面积=1/2πr²-r²=r²(1/2π-1)
=16×(1.57-1)=9.12
例3.
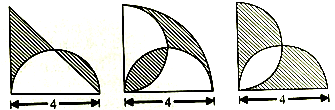
如图,图中的三角形都是等腰直角三角形,求各图阴影部分的面积。(π取3.14)
解析:
通过拆分和重组,得到下列图形。
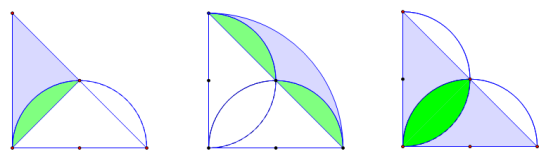
通过拆分和重组,阴影面积转化为了规则的图形。
第1张图片的阴影面积=三角形面积=4×2÷2=4;
第2张图片的阴影面积=弓形面积=扇形-三角形=π/4×4²-4×4÷2=4.56
第3张图片的阴影面积=三角形面积=4×4÷2=8;
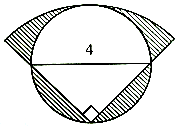
例4.
如图(1)是一个直径是3厘米的半圆,AB是直径。如图(2)所示,让A点不动扇形面积公式3个,把整个半圆逆时针转60°,此时B点移动到C点,请问图中阴影部分的面积是多少平方厘米?
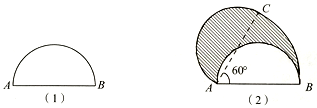
解析:
图形2的总面积=以AB为半径60°的扇形+以AC为直径的半圆。
空白部分的面积=以AB为直径的半圆。
因为图形是由半圆旋转得到,所以AC=AB。

通过重组把不规则的阴影转换成了规则的扇形
根据阴影=整体-空白,可得阴影面积=以AB为半径的60°扇形面积=60/360×πr²=1/6×π×9=1.5π。
例5.
A是半径为3的圆O外一点,弦BC∥AO且BC=3。连接AC、AB,求阴影部分的面积。(π取3.14)
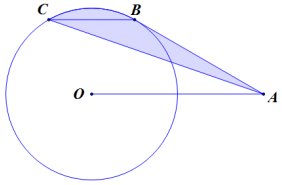
解析:
连接OC和OB,由于BC∥AO,所以S△OBC=S△ABC,则阴影部分面积等于扇形OBC的面积。
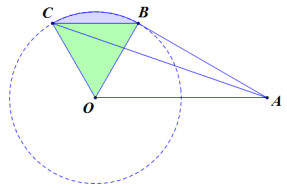
△OBC为等边三角形,扇形的圆心角为60°,则S阴影=πr²×1/6=4.71。
例6.
如图,在半径为4厘米的圆中有两条互相垂直的线段,阴影部分面积A与其他部分面积B之差(大减小)是 平方厘米。
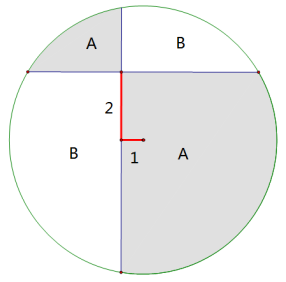
解析:
把图形做下列拆分和重组:
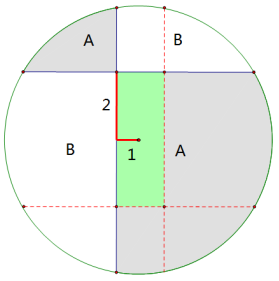
可以看出A-B=绿色长方形面积=1×2×4=8平方厘米。
-3-
练习题
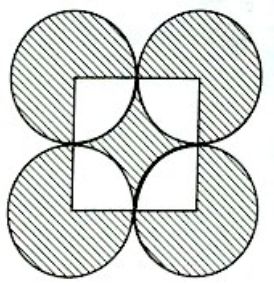
1、图中4个圆的圆心恰好是正方形的4个顶点,如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?
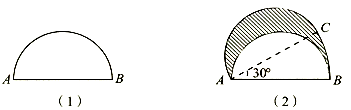
2、如图(1)是一个直径是3厘米的半圆,AB是直径。如图(2)所示,让A点不动,把整个半圆逆时针转30°扇形面积公式3个,此时B点移动到C点,请问图中阴影部分的面积是多少平方厘米?
3、如图三角形ABC为等边三角形,边长为2,D为BC边的中点。分别以B、C为圆形,1为半径作两个扇形(即图中阴影部分)。那么阴影部分的面积是多少?
4、如图是由一个圆与一个直角扇形重叠组成的,其中圆的直径与扇形的半径都是4。图中阴影部分的面积是多少?
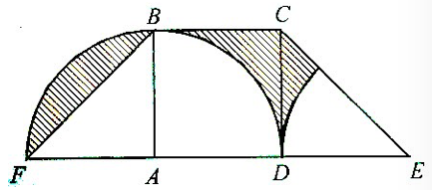
5、如图,ABCD是正方形,且FA=AD=DE=1,阴影部分的面积是多少?
6、求下图阴影的面积。

注意事项:
1、拆分和重组是重点,要仔细观察图形,熟记常见的几何模型。
2、如果需要计算π的具体值,把π的换算放到最后一步,可以减少计算量。
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: Lgxmw666






