导数(或微分)是微积分学中的基本概念之一,是描述函数值随自变量值变化快慢的重要工具。
导数的定义基于极限概念,与函数的值域、单调性、极值等性质密切相关。
本文将介绍基本初等函数的微分公式及微分运算法则幂函数求导,帮助读者更好地理解和应用导数。
一、基本初等函数的微分公式

1. 常数函数的微分公式:若函数f(x)=C(常数),则f'(x)=0。
2. 幂函数的微分公式:若函数f(x)=x^n(n为正整数),则f'(x)=nx^(n-1)。
3. 指数函数的微分公式:若函数f(x)=e^x,则f'(x)=e^x。

4. 对数函数的微分公式:若函数f(x)=log_a(x)(a为正实数且a>1),则f'(x)=1/xln(a)。
5. 三角函数的微分公式:若函数f(x)=sin(x),则f'(x)=cos(x);
若函数f(x)=cos(x),则f'(x)=-sin(x)。

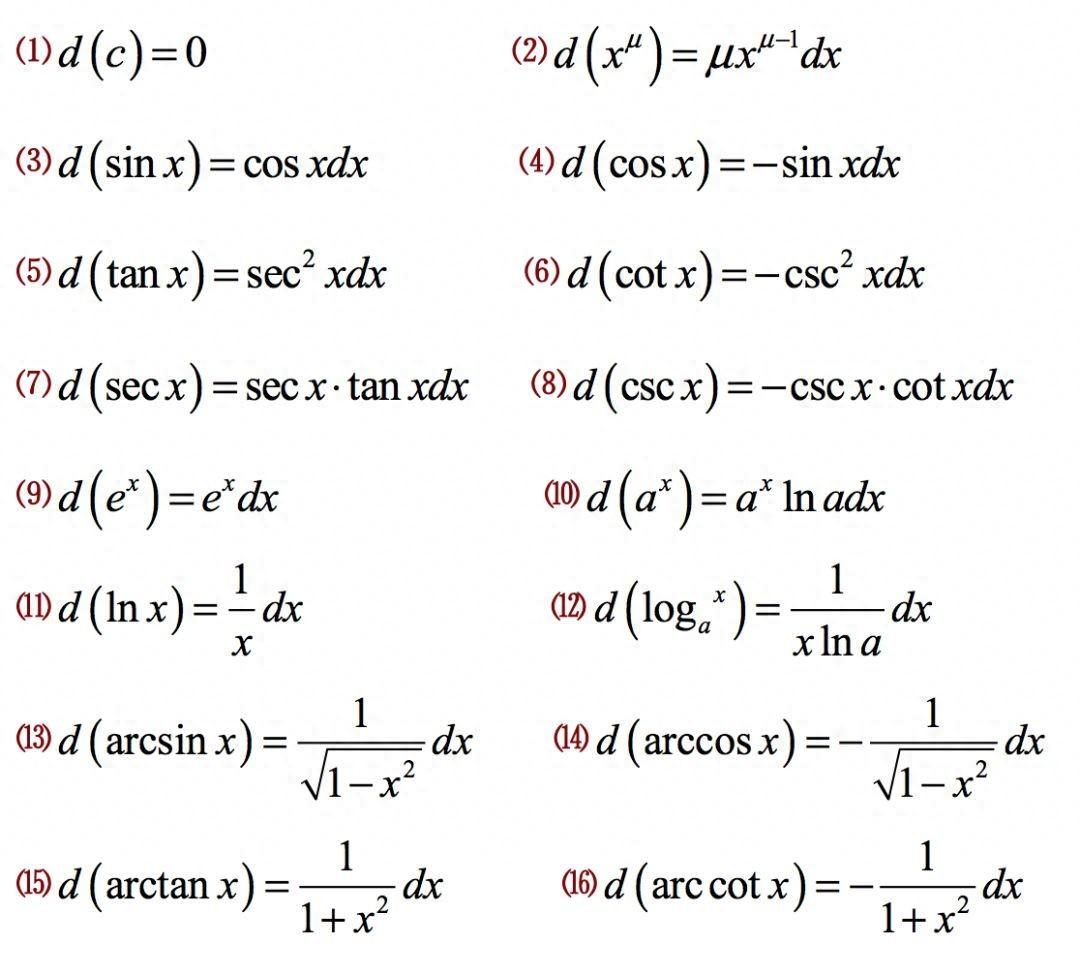
二、微分运算法则
1. 加法法则:若函数f(x)和g(x)可导,则它们的和函数f(x)+g(x)也可导,且其导数为f'(x)+g'(x)。

2. 减法法则:若函数f(x)和g(x)可导,则它们的差函数f(x)-g(x)也可导,且其导数为f'(x)-g'(x)。
3. 乘法法则:若函数f(x)和g(x)可导,则它们的积函数f(x)g(x)也可导,且其导数为f'(x)g(x)+f(x)g'(x)。
4. 除法法则:若函数f(x)和g(x)可导,且g(x)≠0,则它们的商函数f(x)/g(x)也可导,且其导数为[f'(x)g(x)-f(x)g'(x)]/g^2(x)。
5. 复合函数的求导法则:若函数u=g(x)可导,且y=f(u)也可导,则复合函数y=f[g(x)]也可导,且其导数为f'(u)·g'(x)。
6. 反函数的求导法则:若函数y=f(x)单调且可导,则其反函数x=g(y)也可导幂函数求导,且其导数为1/f'(x)。
7. 幂函数的求导法则:若函数y=xn(n为正整数),则其导数为ny^(n-1)。
8. 指数函数的求导法则:若函数y=e^u,则其导数为y'=(e^u)'=e^u。

———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: Lgxmw666