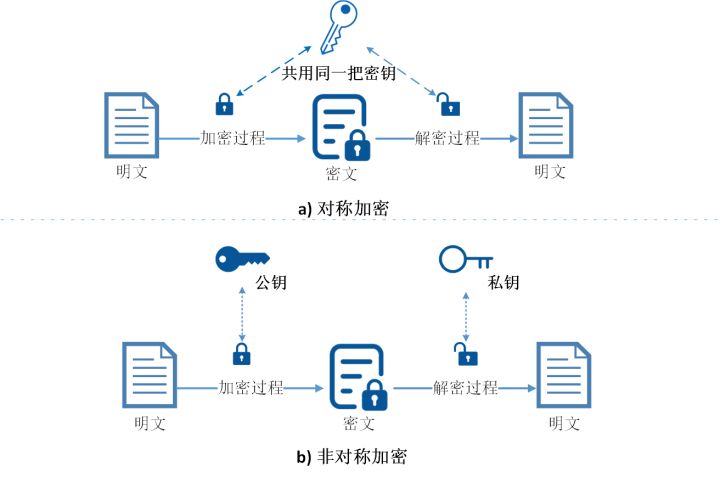
随机数在软件的应用非常广泛。比如说抽奖程序就是一下能想到的应用之一。但是在一些更加重要的应用当中随机数也发挥着重要的作用,比如加密敏感信息、对地球天气等复杂系统建模以及数据的公正采样等都离不开随机数。
不过计算机生成随机数要比掷筛子困难得多,而且那些随机数实际上并不是完全不可预测的,而是在随机种子的基础上结合算法自动生成的的数,这些数实际上是可复制的,算不上真正的随机(伪随机数)。所以随机数的随机性问题是基础算法面临的一大难题。
不过最近德州大学的两位计算机科学家 Eshan Chattopadhyay 和 David Zuckerman 开发出了一种改进的随机抽取器,这种算法只需要两种随机性不强的来源即可生成真正随机的数字,被认为是基础算法取得的一大突破。
一般的随机算法为了提高随机性会在算法中引入环境的随机性,比如鼠标或键盘的位置等。计算机会采样若干时间点的鼠标位置然后转化为一串数字。但这仍然算不上真正的随机随机数法,比如前一刻鼠标位置如果是在屏幕左侧的话,下一刻鼠标跑到右侧的可能性是很低的。因此这样生成的随机数序列仍然具有相关性的,或者是可能会偏向特定值的。也就是说,这种随机性还是很弱。
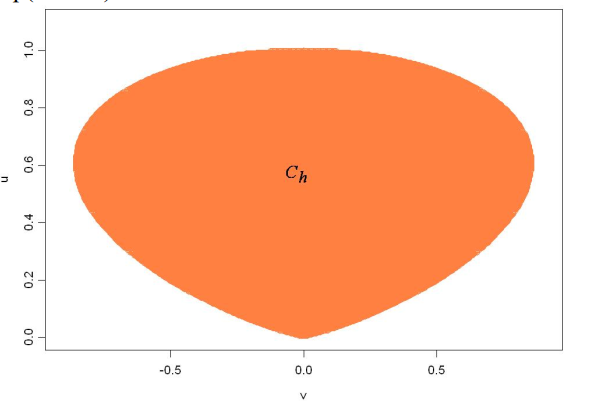
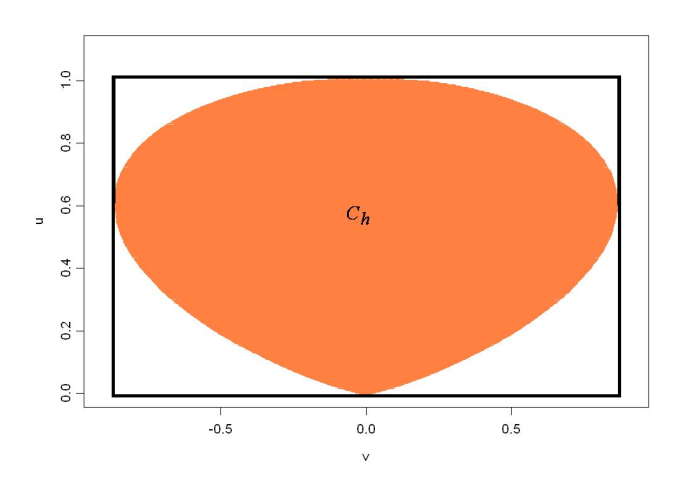
而随机抽取器则是通过这些随机性较弱的来源来发掘随机性。用 MIT 计算机科学家 Dana Moshkovitz 的话来说,随机性是一种资源,获取随机性的过程就像是挖金矿一样—先开采矿石,然后排沙简金。
而两位科学家的算法是对随机抽取器的改进。这种随机抽取器将两种独立的弱随机数来源组合为一个接近随机的集合随机数法,并且只有细微偏差。然后再利用弹性函数(一种信息组合方法)将一串数字转化为真正的随机位—1 或 0。
利用弹性函数进行信息组合可以防止偏差的出现。比方说在大选里面,一些蓄意的投票者有可能会把结果引向想要的方向。但弹性函数可以保护诚实的投票者。因为它不是选取简单多数,而是先把数据分成 3 组,然后选取每组中的多数,再把选出来的数分成 3 组然后再抽取每组中的多数,以此类推直到最后。这种做法使得选举可以容忍大量坏家伙的存在,而在随机数生成方面,这种做法可以把偏差数过滤掉。
跟以往需要接近随机输入的随机抽取器相比,这种新的办法正是通过在随机性非常非常弱的来源当中 “淘金” 来挖掘真正的随机数,从而实现了随机性的实质性改进,其结果已经接近于理想情况。对于加密、复杂系统模拟等应用来说,这是一个非常好的消息。
———END———
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: Lgxmw666